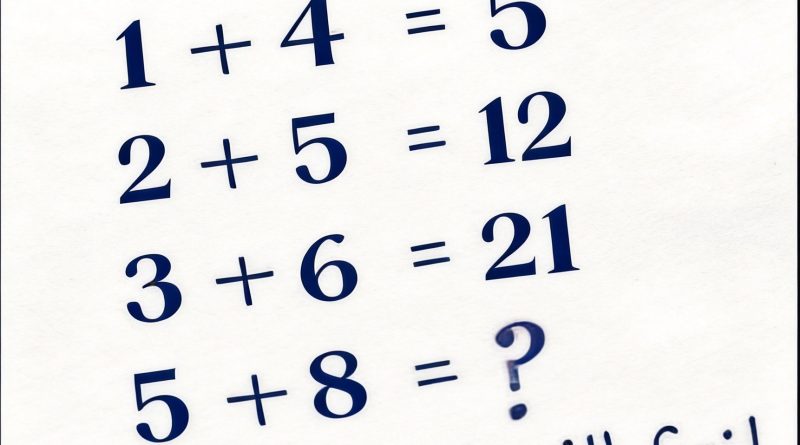Internet Users Can’t Agree on the Answer to This Math Problem
If you’re like many people, the days of sitting in a classroom and solving endless math problems feel like a distant memory.
For some, numbers and formulas evoke a sense of curiosity and enjoyment, while for others, the mere mention of arithmetic can cause anxiety or boredom.
Yet, despite decades of moving away from traditional math exercises, the internet has created a new space for people to engage with numbers — in the form of brain teasers, puzzles, and logic challenges.
What’s remarkable is how these puzzles, often deceptively simple in appearance, can capture our attention for hours, igniting debate and discussion across forums, social media platforms, and online communities.
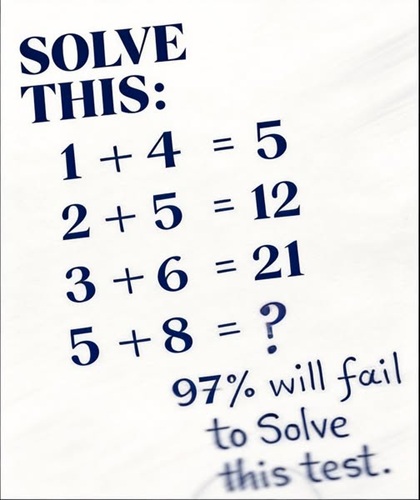
One of the most talked-about math puzzles in recent months has been the seemingly simple sequence:
1 + 4 = 5
2 + 5 = 12
3 + 6 = 21
5 + 8 = ?
At first glance, it looks like a basic arithmetic problem — straightforward addition that even a beginner might be able to solve. But the puzzle quickly becomes puzzling the moment you try to apply conventional rules of addition.
The results clearly don’t match standard arithmetic: 2 + 5 certainly does not equal 12, and 3 + 6 is not 21. This discrepancy is what makes the puzzle so intriguing.
It requires the solver to step outside the realm of normal addition and look for patterns, relationships, or hidden rules.
Why This Puzzle Captures Attention
This puzzle is a classic example of what mathematicians and educators call a “pattern problem” or “sequence puzzle.” The challenge doesn’t lie in performing arithmetic correctly, but in recognizing the underlying rule that governs the transformations.
These types of puzzles appeal to a wide audience because they combine logic, creativity, and reasoning skills — attributes that extend beyond pure mathematics.
The popularity of this puzzle is evident across online platforms like Reddit, Quora, and various brain-teaser websites, where thousands of users have attempted to solve it.
Some approach it analytically, testing different mathematical operations like multiplication, division, or factorials. Others take a more creative route, interpreting the “+” sign not as addition but as a signal for a sequence-based rule or cumulative operation.
This diversity of approaches explains why so many different answers appear online, each with its own justification.
Exploring Different Approaches
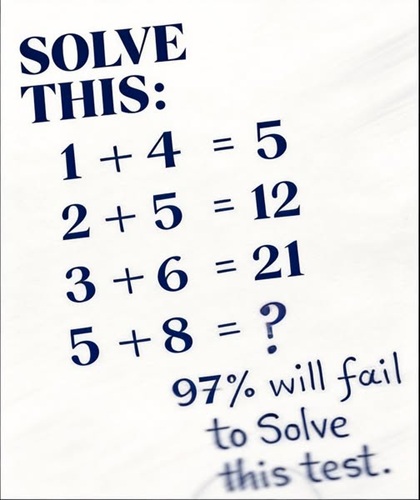
To understand why this puzzle is so divisive, let’s examine some of the most common interpretations:
1. The Cumulative Sum Method
One popular method involves building on previous results. Here, the pattern is understood as:
Result = A + (B × previous result)
Applying this rule step by step:
-
1 + 4 = 5
Since there is no previous result, we simply take the first line as given. -
2 + 5 = ?
Multiply 5 (B) by the previous result (5 from the first equation): 5 × 5 = 25.
Add 2 (A): 25 + 2 = 27. -
3 + 6 = ?
Multiply 6 (B) by the previous result (27 from the second equation): 6 × 27 = 162.
Add 3 (A): 162 + 3 = 165. -
5 + 8 = ?
Multiply 8 (B) by the previous result (165): 8 × 165 = 1320.
Add 5 (A): 1320 + 5 = 1325.
This method produces a sequence that grows rapidly, and while it may seem extreme, it highlights how a single change in rule interpretation can drastically affect the outcome. It also demonstrates that these puzzles test flexibility of thinking more than basic arithmetic.
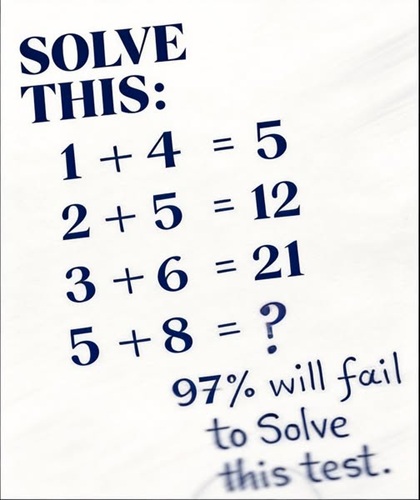
2. The “Add and Multiply” Rule
Another approach interprets the problem as:
Result = (A × B) + A
Step by step:
-
1 + 4 = (1 × 4) + 1 = 4 + 1 = 5 ✅
-
2 + 5 = (2 × 5) + 2 = 10 + 2 = 12 ✅
-
3 + 6 = (3 × 6) + 3 = 18 + 3 = 21 ✅
-
5 + 8 = (5 × 8) + 5 = 40 + 5 = 45 ✅
This method is perhaps the most widely cited “correct” answer for those approaching the puzzle with a clean mathematical formula.
It explains the pattern in a logical, repeatable way and produces results consistent with the first three lines. For many puzzle enthusiasts, this solution is both satisfying and elegant because it balances simplicity and creativity.
3. Adding the Previous Result
A third approach interprets the puzzle as adding the previous result to the next sum:
Following this logic:
-
1 + 4 = 5 ✅
-
2 + 5 + 5(previous result) = 2 + 5 + 5 = 12 ✅
-
3 + 6 + 12(previous result) = 3 + 6 + 12 = 21 ✅
-
5 + 8 + 21(previous result) = 5 + 8 + 21 = 34 ✅
This method produces 34 as the answer. It is slightly less intuitive than the multiply-and-add approach but is widely accepted among those who focus on cumulative sequencing rather than operations on each individual pair.
4. Binary or Alternate Number Systems
Some creative solvers have experimented with representing the numbers in binary, hexadecimal, or other numeral systems to extract hidden patterns. For example, interpreting results as binary sums or sequences often produces answers like 1101 or 111, depending on the base conversion used.
While less conventional, these methods illustrate the flexibility of thought these puzzles inspire and why they can be both fun and frustrating at the same time.
Why There’s No Single “Correct” Answer
What makes this puzzle so fascinating is that there isn’t a universally agreed-upon solution. Depending on the assumptions you make about the pattern — whether you focus on multiplication, cumulative addition, or another sequence rule — the answer changes.
This ambiguity is a central part of the puzzle’s appeal: it challenges solvers to think beyond traditional arithmetic and consider creative ways numbers can relate to each other.
For educators and puzzle enthusiasts, this puzzle is a perfect example of how logic and pattern recognition can be more important than raw calculation skills.
It’s also a reminder that many problems in mathematics and real life do not have a single solution — instead, they encourage multiple methods of reasoning and problem-solving.
Online Debate and Public Reaction
The puzzle has sparked intense debate online, with thousands of posts analyzing the possible answers. Some users confidently argue for 45 as the answer using the multiply-and-add formula, while others defend 34 or even more unusual outcomes.
On social media platforms like Reddit, X (formerly Twitter), and Facebook groups, users have shared diagrams, step-by-step calculations, and even memes illustrating different approaches.
One popular discussion thread on Reddit has over 50,000 comments, with participants debating whether the puzzle’s intention was purely mathematical or more of a “brain teaser” designed to test lateral thinking.
Some commenters pointed out that puzzles like this are valuable not for finding a single correct answer but for encouraging critical thinking, reasoning, and debate.
Examples of Public Reactions
-
“I got 45, but honestly, I could see 34 working too. This puzzle is so fun because it makes you think in different ways.”
-
“At first, I thought it was simple addition… then I realized that’s not even close. My brain hurts.”
-
“I tried doing it in binary just for fun, and somehow I ended up with 1101. Math is wild.”
-
“These puzzles are great for teaching kids about sequences and patterns. It’s not about getting the answer right, it’s about understanding the logic.”
These reactions underscore the social and educational value of seemingly trivial math puzzles. Beyond being an entertaining challenge, they spark dialogue, collaboration, and problem-solving discussions across a diverse group of people.
Lessons From the Puzzle
Aside from the challenge itself, this puzzle offers several broader lessons:
-
Patterns Matter More Than Numbers Alone
Numbers themselves are only meaningful within the framework of a rule or pattern. Recognizing relationships, sequences, and formulas is often more critical than basic arithmetic. -
Multiple Perspectives Can Lead to Multiple Solutions
A problem may have more than one valid solution, depending on how you interpret the rules. This encourages flexibility in thinking and openness to alternative methods. -
Logic and Creativity Work Together
Solving the puzzle requires both analytical reasoning and imaginative thinking. Creative approaches, such as considering cumulative results or alternate numerical systems, often reveal solutions that pure calculation does not. -
Communication and Explanation Are Key
Many people reach an answer but struggle to explain their reasoning. Part of the fun is writing out the steps and seeing how others approach the same problem differently. -
Enjoy the Process
Perhaps most importantly, this puzzle reminds us that mathematics can be playful, social, and intriguing, even outside the classroom. It’s less about the “right” answer and more about the thinking journey. -
Applying This Type of Thinking Beyond Math
The skills used to tackle puzzles like this — spotting patterns, considering alternative rules, and thinking creatively — are widely applicable in other areas of life.
From coding and data analysis to everyday problem-solving, the ability to identify patterns and test different hypotheses is invaluable.
For example:
-
In technology, understanding sequences and algorithms mirrors how computers process operations and predict outcomes.
-
In finance, recognizing patterns in data can inform investment decisions or risk analysis.
-
In everyday life, spotting repetitive behaviors or trends can help in planning schedules, optimizing workflows, or troubleshooting problems.
- Conclusion
The “1 + 4 = 5” puzzle is more than a simple arithmetic challenge. It’s a brain teaser that encourages lateral thinking, pattern recognition, and discussion, making it a favorite on social media and online forums.
Its appeal lies not just in finding an answer, but in the variety of methods and reasoning it inspires. Whether your solution is 45, 34, 32, 111, 1101, or some other interpretation entirely, the puzzle succeeds in engaging minds and fostering curiosity.
Ultimately, this type of puzzle demonstrates that mathematics isn’t just about memorizing formulas or performing calculations — it’s about exploring possibilities, testing ideas, and learning to see the world through multiple lenses.
So next time you encounter a problem that seems deceptively simple, remember: sometimes the journey to understanding is far more rewarding than the answer itself.
So, what answer did you get? More importantly, how did you think through the pattern? And did the process teach you something new about the way numbers and logic interact in the real world?
Whether it’s 45, 34, or something else entirely, this puzzle proves that even the simplest-looking math problem can spark hours of curiosity, debate, and intellectual fun.